Neuronal Dynamics (8)
Noisy Input Models: Barrage of Spike Arrivals
The online version of this chapter:
Chapter 8 Noisy Input Models: Barrage of Spike Arrivals https://neuronaldynamics.epfl.ch/online/Ch8.html
Noise input
Modeling the noisiness of the input amounts to splitting the input current into two components, a deterministic and a stochastic one \[ I(t)=I^{det}(t)+I^{noise}(t), \tag{8.1} \]
\(I^{det}\): known or at least predictable. \(I^{noise}\): unpredictable or noisy.
For example, during an in vitro study with intracellular current injection, \(I^{det}\) would be the current that is set on the switchboard of the current generator, but the actual current fluctuates around the preset value because of finite temperature.
A nonlinear integrate-and-fire model with noisy input has the voltage equation \[ \tau_m\frac{\mathrm{d}}{\mathrm{d}t}u=f(u)+RI^{det}(t)+RI^{noise}(t). \tag{8.2} \] If \(u\) reaches the threshold \(\theta_{reset}\), the integration is stopped and the membrane potential reset to \(u_r\).
White noise
Formulate the noise term \(RI^{noise}\) in the differential equation of the membrane voltage as a 'white noise', \(RI^{noise}(t)=\xi(t)\). White noise \(\xi\) is a stochastic process characterized by its expectation value, \[ \langle \xi(t) \rangle =0, \tag{8.3} \] and the autocorrelation \[ \langle \xi(t)\xi(t')\rangle=\sigma^{2} \tau_m \delta(t-t'), \tag{8.4} \] where \(\sigma\) is the amplitude of the noise (in units of voltage) and \(\tau_m\) the time constant of (8.2). (8.4) indicates that the process \(\xi\) is uncorrelated in time: knowledge of the value \(\xi\) at time \(t\) does not enable us to predict its value at any other time \(t'\neq t\).
The Fourier transform of the autocorrelation function (8.4) yields the power spectrum. The power spectrum of white noise is flat, i.e., the noise is equally strong at all frequencies.
Stochastic differential equation, i.e., an equation for a stochastic process, \[ \tau_m \frac{\mathrm{d}}{\mathrm{d}t}u(t)=f(u(t))+RI^{det}(t)+\xi(t), \tag{8.5} \] also called Langevin equation.
In the mathematical literature, a different style of writing the Langevin equation dominates. \[ \mathrm{d}u=f(u)\frac{\mathrm{d}t}{\tau_m}+RI^{det}(t)\frac{\mathrm{d}t}{\tau_m}+\sigma \mathrm{d}W_{t}, \tag{8.6} \] where \(\mathrm{d}W_{t}\) are the increments of the Wiener process in a short time \(\mathrm{d}t\), that is, \(\mathrm{d}W_{t}\) are random variables drawn from a Gaussian distribution with zero mean and variance proportional to the step size \(\mathrm{d}t\) (therefore its standard deviation is proportional to \(\sqrt{\mathrm{d}t}\)). White noise which is Gaussian distributed is called Gaussian white noise.
Example: Leaky integrate-and-fire model with white noise input
In the case of the leaky integrate-and-fire model (with voltage scale chosen such that the resting potential is at zero), the stochastic differential equation is \[ \tau_m \frac{\mathrm{d}}{\mathrm{d}t}u(t)=-u(t)+RI^{det}(t)+\xi(t), \tag{8.7} \] which is called the Ornstein-Uhlenbeck process.
The fluctuates of the membrane potential have an autocorrelation with characteristic time \(\tau_m\).
Noisy versus noiseless membrane potential
Consider (8.7) for constant \(\sigma\). At \(t=\hat{t}\) the membrane potential starts at a value \(u=u_r=0\). The solution for \(t>\hat{t}\) is \[ u(t)=\frac{R}{\tau_m}\int_{0}^{t-\hat{t}} \mathrm{e}^{-s/\tau_m} I^{det}(t-s) \mathrm{d}s+\frac{1}{\tau_m}\int_{0}^{t-\hat{t}} \mathrm{e}^{-s/\tau_m} \xi(t-s) \mathrm{d}s. \] (8.9)
Since \(\langle \xi(t)\rangle=0\), the expected trajectory of the membrane potential is \[ u_0(t)=\langle u(t|\hat{t})\rangle=\frac{R}{\tau_m}\int_{0}^{t-\hat{t}} \mathrm{e}^{-s/\tau_m} I^{det}(t-s) \mathrm{d}s. \] (8.10)
In particular, for constant input current \(I^{det}(t)\equiv I_0\) we have \[ u_0(t)=u_{\infty}[1-\mathrm{e}^{-(t-\hat{t})/\tau_m}] \tag{8.11} \] with \(u_{\infty}=RI_0\).
The variance \(\langle \Delta u^{2}\rangle\) can be evaluated as \[ \langle \Delta u^{2}(t)\rangle =\frac{1}{\tau_m^{2}}\int_{0}^{t-\hat{t}} \int_{0}^{t-\hat{t}} \mathrm{e}^{-s/\tau_m} \mathrm{e}^{-s'/\tau_m} \langle \xi(t-s)\xi(t-s')\rangle \mathrm{d}s' \mathrm{d}s \] (8.12)
We use \(\langle \xi(t-s)\xi(t-s')\rangle=\sigma^{2}\tau_m\delta(s-s')\) and perform the integration. The result is \[ \langle \Delta u^{2}(t)\rangle=\frac{1}{2}\sigma^{2}\left[1-\mathrm{e}^{-2(t-\hat{t})/\tau_m} \right] \tag{8.13} \]
If the threshold is high enough so that firing is a rare event, the typical distance between the actual trajectory and the mean trajectory approaches with time constant \(\tau_m/2\) a limiting value \[ \sqrt{\langle \Delta u_{\infty}^{2}\rangle}=\frac{1}{\sqrt{2}}\sigma. \tag{8.14} \]
Colored Noise
A noise term with a power spectrum which is not flat is called colored noise. Colored noise \(I^{noise}(t)\) can be generated from white noise by suitable filtering. For example, low-pass filtering \[ \tau_s \frac{\mathrm{d}I^{noise}(t)}{\mathrm{d}t}=-I^{noise}(t)+\xi(t), \tag{8.15} \] where \(\xi(t)\) is the white noise process.
Integrate (8.15) so as to arrive at \[ I^{noise}(t)=\int_{0}^{\infty} \kappa(s)\xi(t-s) \mathrm{d}s, \tag{8.16} \]
where \(\kappa(s)\) is an exponential low-pass filter with time constant \(\tau_s\) (Actually \(\kappa(s)=\exp (-s/\tau_s)/\tau_s\)). The autocorrelation function is therefore \[ \langle I^{noise}(t)I^{noise}(t')\rangle =\int_{0}^{\infty} \int_{0}^{\infty} \kappa(s)\kappa(s')\langle \xi(t-s)\xi(t'-s')\rangle \mathrm{d}s' \mathrm{d}s. \] (8.17)
We exploit the definition of the white noise correlation function in (8.4) and find \[ \langle I^{noise}(t)I^{noist}(t')\rangle=a \exp \left(-\frac{\lvert t-t' \rvert }{\tau_s}\right) \tag{8.18} \] with a amplitude factor \(a\). That means knowledge of the input current at time \(t\) gives us a hint about the input current shortly afterward, as long as \(\lvert t'-t \rvert \ll \tau_s\).
The noise spectrum is flat for frequencies \(\omega\ll 1/\tau_s\) and falls off for \(\omega>1/\tau_s\). Sometimes \(1/\tau_s\) is called the cut-off frequency.
Stochastic spike arrival
If we focus on a leaky integrate-and-fire neuron, shift the voltage so that the resting potential is at zero and concentrate on a single neuron receiving stochastic input from background neurons hence drop the input from the network, we arrive at \[ \frac{\mathrm{d}}{\mathrm{d}t}u=-\frac{u}{\tau_m}+\frac{1}{C}I^{ext}(t)+\sum_{k}^{} \sum_{t_k^{(f)}}^{} w_k \delta(t-t_k^{(f)}) \] (8.20)
The membrane potential is reset to \(u_r\) whenever is reaches the threshold \(\theta\). (8.20) is called Stein's model.
In Stein's model, each input spike generates a postsynaptic potential \(\Delta u(t)=w_k \epsilon(t-t^{(f)}_k)\) with \(\epsilon(s)=\mathrm{e}^{-s/\tau_m} \Theta(s)\). Integration of (8.20) yields \[ u(t|\hat{t})=u_r \exp (-\frac{t-\hat{t}}{\tau_m})+\frac{1}{C}\int_{0}^{t-\hat{t}} \exp (-\frac{s}{\tau_m})I(t-s) \mathrm{d}s+\sum_{k=1}^{N} \sum_{t_k^{(f)}}^{} w_k \epsilon(t-t_k^{(f)}) \] (8.21)
for \(t>\hat{t}\) where \(\hat{t}\) is the last firing time of the neuron.
Membrane potential fluctuations caused by spike arrivals
We assume that each input spike evokes a postsynaptic potential \(w_0 \epsilon(s)\) of the same amplitude and shape, independent of \(k\). The input statistics is assumed to be Poisson. Thus, the total input spike train \[ S(t)=\sum_{k=1}^{N} \sum_{t_k^{(f)}}^{} \delta(t-t_k^{f}), \tag{8.22} \] that arrives at neuron \(i\) is a random process with expectation \[ \langle S(t)\rangle =\nu_0 \tag{8.23} \] and autocorrelation \[ \langle S(t)S(t')\rangle=\nu_0^{2}+\nu_0 \delta(t-t'); \tag{8.24} \]
Suppose that we start theh integration of the passive membrane equation at \(t=-\infty\) with initial condition \(u_r=0\). We rewrite (8.21) using the definition of the spike trian in (8.22) \[ u(t)=\frac{1}{C}\int_{0}^{\infty} \exp \left(-\frac{s}{\tau_m}\right)I(t-s) \mathrm{d}s+w_0 \int_{0}^{\infty} \epsilon(s)S(t-s) \mathrm{d}s. \tag{8.25} \]
Using (8.23) and (8.24) we find \[ \langle u(t)\rangle=u_0(t)=\frac{1}{C}\int_{0}^{\infty} \exp \left(-\frac{s}{\tau_m}\right)I(t-s) \mathrm{d}s+w_0\nu_0 \int_{0}^{\infty} \epsilon(s) \mathrm{d}s \tag{8.26} \] and \[ \langle \Delta u^{2}\rangle=\langle [u(t)-u_0(t)]^{2}\rangle = w_0^{2}\nu_0 \int_{0}^{\infty} \epsilon^{2}(s) \mathrm{d}s. \]
With stochastic spike arrival at excitatory synapses, mean and variance cannot be changed independently. As we will see next, a combination of excitation and inhibition allows us to increase the variance while keeping the mean of the potential fixed.
Balanced excitation and inhibition
Suppose we have excitatory input and inhibitory input of the same frequency. The mean of the stochastic background input vanishes since \(\sum_{k}^{} w_k v_k=0\). The stochastic arrival of background spikes generates fluctuations of the voltage with variance \[ \langle \Delta u^{2}\rangle=\frac{1}{2}\tau_m \sum_{k}^{} w_k^{2}\nu_k \]
Let us now increase all rates by a factor of \(a>1\) and multiply at the same time the synaptic efficacies by a factor \(1/\sqrt{a}\). Then both mean and variance of the stochastic background input are the same as before, but the size \(w_k\) of the jumps is decreased.
In the limite of \(a\to \infty\) the jump process turns into a diffusion process. The diffusion limit: \[ \frac{w}{\sqrt{a}}S^{exc}-\frac{w}{\sqrt{a}}S^{inh} \to \xi(t) \tag{8.31} \]
Example: Synaptic time constants and colored noise
In contrast to the previous discussion of balanced input, we now assume that each spike arrival generated a current pulse \(\alpha(s)\) of finite duration so that the total synaptic input current is \[ RI(t)=w^{exc}\int_{0}^{\infty} \alpha(s)S^{exc}(t-s) \mathrm{d}s - w^{inh} \int_{0}^{\infty} \alpha(s)S^{inh}(t-s) \mathrm{d}s \] (8.32)
If the spike arrivel is Poisson with rates \(a\nu\) and the synaptic weights are \(w^{exc}=w^{inh}=w/\sqrt{a}\), then we can take the limit \(a\to \infty\) with no change of mean or variance. The result is colored noised.
An instructive case is \(\alpha(s)=(1/\tau_s)\exp (-s/\tau_s)\Theta(s)\) with synaptic time constant \(\tau_s\). In the limit \(\tau_s\to 0\) we are back to white noise.
Subthreshold vs. Superthreshold regime
An arbitrary time-dependent stimulus \(I(t)\) is called subthreshold if is generates a membrane potential that stays - in the absence of noise - below the firing threshold. Stimuli that induce spikes even in a noise-free neuron are called superthreshold.
The distinction between sub- and superthreshold stimuli has important consequences for the firing behavior of neurons in the presence of noise. Consider a leaky integrate-and-fire neuron with constant input \(I_0\) for \(t>0\). \[ u_0(t)=u_{\infty}[1-\mathrm{e}^{-t/\tau_m} ]+u_r\mathrm{e}^{-t/\tau_m} . \tag{8.33} \] where \(u_{\infty}=RI_0\). If \(u_{\infty}>\theta\), the neuron fires regularly. The interspike interval is \(s_0\) derived from \(u_0(s_0)=\theta\). Thus \[ s_0=\tau \ln \frac{u_{\infty}-u_r}{u_{\infty}-\theta}. \tag{8.34} \]
In the superthreshold regime, the spike train in the presence of diffusive noise is simply a noisy version of the regular spike train of the noise-free neuron.
Example: Interval distribution in the superthreshold regime
For small noise amplitude \(0<\sigma\ll u_{\infty}-\theta\), and superthreshold stimulation, the interval distribution is centered at the deterministic interspike interval \(s_0\). As long as the mean trajectory is far away from the threshold, the distribution of membrane potentials has a Gaussian shape. As time goes on, the distribution of membrane potentials is pushed across the threshold.
Suppose the membrane potential crosses the threshold with slope \(u_0'\), then the interval distribution is approximately given by a Gaussian with mean \(s_0\) and width \(\sigma/\sqrt{2}u_0'\), i.e., \[ P_0(t|0)=\frac{1}{\sqrt{\pi}}\frac{u_0'}{\sigma}\exp \left[-\frac{(u_0')^{2}(t-s_0)^{2}}{\sigma^{2}}\right] \tag{8.35} \]
Diffusion limit and Fokker-Planck equation
In this section we analyze (8.20) and show how to map it to the diffusion model. The evolution of the probability density as a function of time is described, in the diffusion limit, by the Fokker-Planck equation. We derive here in the context of a single neuron subject to noisy input.
For simplicity we set for the time being \(I^{ext}=0\) in (8.20). The input spikes at synapse \(k\) are generated by a Poisson process and arrive stochastically with rate \(\nu_k(t)\). The probability that no spike arrives in a short time interval \(\Delta t\) is therefore \[ \operatorname{Pr} \{\text{no spike in}\ [t,t+\Delta t]\}=1-\sum_{k}^{} \nu_k(t)\Delta t. \tag{8.36} \]
Given a value of \(u'\) at time \(t\), the probability density of finding a membrane potential \(u\) at time \(t+\Delta t\) is given by \[ \begin{aligned} P^{trans}(u,t+\Delta t|u',t)=\left[1-\Delta t \sum_{k}^{} \nu_k(t)\right]\delta(u-u' \mathrm{e}^{-\Delta t/\tau_m})\\+\Delta t \sum_{k}^{} \nu_k(t)\delta(u-u'\mathrm{e}^{-\Delta t/\tau_m} -w_k). \\ \end{aligned} \] (8.37)
We will refer to \(P^{trans}\) as the transition law. The evolution of the membrane potential is a Markov Process and can be described by \[ p(u,t+\Delta)=\int_{}^{} P^{trans}(u,t+\Delta t|u',t)p(u',t) \mathrm{d}u'. \tag{8.38} \]
Recall that \(\delta(au)=a^{-1}\delta(u)\). The result of the integration is \[ \begin{aligned} p(u,t+\Delta t)=\left[ 1-\Delta t \sum_{k}^{} \nu_k(t)\right]\mathrm{e}^{\Delta t/\tau_m} p(\mathrm{e}^{\Delta t/\tau_m} u,t) \\ +\Delta t\sum_{k}^{} \nu_k(t)\mathrm{e}^{\Delta t/\tau_m} p(\mathrm{e}^{\Delta t/\tau_m}( u-w_k),t). \end{aligned} \] (8.39)
So we have \[ \frac{\partial p(u,t)}{\partial t}==\frac{1}{\tau_m}p(u,t)+\frac{1}{\tau_m}u\frac{\partial }{\partial u}p(u,t)+\sum_{k}^{} \nu_k(t)[p(u-w_k,t)-p(u,t)]. \] (8.40)
Furthermore, if the jump amplitudes \(w_k\) are small, we can expand the RHS of (8.40) with respect to \(u\) about \(p(u,t)\): \[ \tau_m \frac{\partial }{\partial t}p(u,t)=-\frac{\partial }{\partial u}\left[-u+\tau_m \sum_{k}^{} \nu_k(t)w_k\right]p(u,t)+\frac{1}{2}\left[\tau_m \sum_{k}^{} \nu_k(t)w_k^{2}\right]\frac{\partial ^{2}}{\partial u^{2}}p(u,t), \] (8.41)
where we have neglected terms of order \(w_k^{3}\) and higher. The expansion in \(w_k\) is called the Kramers-Moyal expansion.
In (8.41), the first term in rectangular brackets describes the systematic drift of the membrane potential due to leakage (\(\propto -u\)) and mean background input (\(\propto \sum_{k}^{} \nu_k(t)w_k\)). The second term in rectangular brackets corresponds to a 'diffusion constant' and accounts for the fluctuations of the membrane potential.
(8.41) is equivalent to the Langevin equation (8.7) with \(RI(t)=\tau_m\sum_{k}^{} \nu_k(t)w_k\) and time-dependent noise amplitude \[ \sigma^{2}(t)=\tau_m\sum_{k}^{} \nu_k(t)w_k^{2}. \tag{8.42} \]
For the transition from (8.40) to (8.41) we have suppressed \[ \sum_{n=3}^{\infty} \frac{(-1)^{n}}{n!}A_n(t)\frac{\partial ^{n}}{\partial u^{n}}p(u,t) \tag{8.43} \] with \(A_n=\tau_m \sum_{k}^{} \nu_k(t)w_k^{n}\).
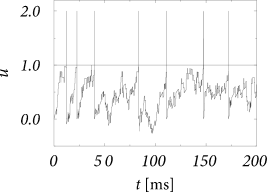
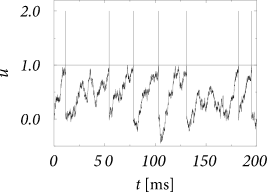
Figures above shows a sequence of models where the size of the weights \(w_k\) decreases so that \(A_n \to 0\) for \(n\geqslant 3\) while the mean \(\sum_{k}^{} \nu_k(t)w_k\) and the second moment \(\sum_{k}^{} \nu_k(t)w_k^{2}\) remain constant. Such a sequence of models does not exist for excitatory input alone.
Threshold and firing
We now incorporate a threshold condition into (8.41) and (8.7). In the Fokker-Planck equation (8.41), the firing threshold is incorporated as a boundary condition \[ p(\theta,t)\equiv 0 \ \text{for all} \ t \]
This boundary condition is only for white noise model. For colored noise the density at threshold is finite, because the effective frequency of 'attempts' to push a neuron which has membrane potential \(\theta-\delta<u\leqslant \theta\) above threshold is limited by the cut-off frequency of the noise.
Example: Free distribution without threshold
The solution of (8.41) with initial condition \(p(u,\hat{t})=\delta(u-u_r)\) is a Gaussian with mean \(u_0(t)\) and variance \(\langle \Delta u^{2}(t)\rangle\), i.e., \[ p(u,t)=\frac{1}{\sqrt{2\pi \langle \Delta u^{2}(t)\rangle}}\exp \left\{-\frac{[u(t|\hat{t})-u_0(t)]^{2}}{2\langle \Delta u^{2}(t)\rangle}\right\} \] (8.45)
In particular, the stationary distribution that is approached in the limit of \(t\to \infty\) for constant input \(I_0\) is \[ p(u,\infty)=\frac{1}{\sqrt{\pi}}\frac{1}{\sigma} \exp \left\{\frac{[u-RI_0]^{2}}{\sigma^{2}}\right\}, \tag{8.46} \] which describes a Gaussian distribution with mean \(u_{\infty}=RI_0\) and variance \(\sigma/\sqrt{2}\).
Interval distribution for the diffusive noise model
Let us consider a leaky integrate-and-fire neuron that starts at time \(\hat{t}\) with a membrane potential \(u_r\) and is driven for \(t>\hat{t}\) by a known input \(I(t)\). We have \[ \operatorname{Pr} \{u_0<u(t)<u_1|u(\hat{t})=u_r\}=\int_{u_0}^{u_1} p(u,t) \mathrm{d}u \tag{8.47} \] where \(p(u,t)\) is the probability density of the membrane potential at time \(t\). In the diffusion limit, \(p(u,t)\) can be found by solution of the Fokker-Planck equation (8.41) with initial condition \(p(u,\hat{t})=\delta(u-u_r)\) and boundary condition \(p(\theta,t)=0\).
Imagine that we run 100 simulation trials. The expected fraction of simulations that have not yet reached the threshold and therefore still 'survive' up to time \(t\) is given by the survivior function, \[ S_{I}(t|\hat{t})=\int_{-\infty}^{\theta} p(u,t) \mathrm{d}u. \tag{8.48} \]
In view of (7.24), the input-dependent interval distribution is therefore \[ P_{I}(t|\hat{t})=-\frac{\mathrm{d}}{\mathrm{d}t}\int_{-\infty}^{\theta} p(u,t) \mathrm{d}u. \tag{8.49} \]
In the context of noisy integrate-and-fire neurons \(P_{I}(t|\hat{t})\) is called the distribution of 'first passage times'. no general solution is known for the first passage time problem of the Ornstein-Uhlenbeck process.
Example: Numerical evaluation of \(P_{I}(t|\hat{t})\)
(8.41) has been solved in the absence of a threshold. The transition probability from an arbitrary starting value \(u'\) at time \(t'\) to a new value \(u\) at time \(t\) is \[ P^{trans}(u,t|u',t')=\frac{1}{\sqrt{2\pi\langle \Delta u^{2}(t)\rangle}}\exp \left\{-\frac{[u-u_0(t)]^{2}}{2\langle \Delta u^{2}(t)\rangle}\right\} \] (8.50)
with \[ u_0(t)=u'\mathrm{e}^{-(t-t')/\tau_m} +\int_{0}^{t-t'} \mathrm{e}^{-s'/\tau_m} I(t-s') \mathrm{d}s \tag{8.51} \]
\[ \langle \Delta u^{2}(t)\rangle=\frac{\sigma^{2}}{2}[1-\mathrm{e}^{-2(t-s)/\tau_m}]. \tag{8.52} \]
Because of the Markov property, the probability density to cross the threshold (not necessarily for the first time) at a time \(t\), is equal to the probability to cross it for the first time at \(t'<t\) and to return back to \(\theta\) at time \(t\), that is, \[ P^{trans}(\theta,t|u_r,\hat{t})=\int_{\hat{t}}^{t} P_{I}(t'|\hat{t})P^{trans}(\theta,t|\theta,t') \mathrm{d}t'. \tag{8.53} \]
Mean interval and mean firing rate (diffusive noise)
Here we express the mean firing rate of a leaky integrate-and-fire model with diffusive noise as a function of a (constant) input \(I_0\).
For constant input \(I_0\) the mean interspike interval is \(\langle s\rangle=\int_{0}^{\infty} sP_{I_0}(s|0) \mathrm{d}s=\int_{0}^{\infty} sP_0(s) \mathrm{d}s\). For the diffusion model (8.7) with threshold \(\theta\), reset potential \(u_r\), and membrane time constant \(\tau_m\), the mean interval is \[ \langle s\rangle=\tau_m \sqrt{\pi}\int_{\frac{u_r-h_0}{\sigma}}^{\frac{\theta-h_0}{\sigma}} \exp (u^{2})[1+\text{erf}(u)] \mathrm{d}u, \tag{8.54} \] where \(h_0=RI_0\) is the input potential caused by the constant current \(I_0\). This expression is sometimes called the Siegert-formula. The inverse of the mean interval is the mean firing rate.