Neuronal Dynamics (5)
Nonlinear Integrate-and-Fire Models
The online version of this chapter:
Chapter 5 Nonlinear Integrate-and-Fire Models https://neuronaldynamics.epfl.ch/online/Ch5.html
Thresholds in a nonlinear integrate-and-fire model
In a general nonlinear integrate-and-fire model with a single variable \(u\), the membrane potential evolves according to \[ \tau \frac{\mathrm{d}}{\mathrm{d}t}u=f(u)+R(u)I. \] (5.2)
The dynamics is stopped if \(u\) reaches the threshold \(\theta_{reset}\). In this case the firing time \(t^{(f)}\) is noted and integration of the membrane potential equation restarts at time \(t^{(f)}+\Delta^{abs}\) with initial condition \(u_{r}\). If not specified otherwise, we always assume a constant input resistance \(R(u)=R\) independent of voltage.
Example: Rescaling and standard forms
Introduce a new variable \(\tilde{u}\) by the transformation \[ u(t) \to \tilde{u}(t)=\tau \int_{0}^{u(t)} \frac{\mathrm{d}x}{R(x)} \] which is possible if \(R(x)\neq 0\) for all \(x\) in the integration range. In terms of \(\tilde{u}\) we have \[ \frac{\mathrm{d}\tilde{u}}{\mathrm{d}t}=d(\tilde{u})+I(t) \] with \(d(\tilde{u})=f(u)/R(u)\).
Where is the firing threshold?
The voltage threshold \(\theta\) determined with pulse-like input currents is different from the voltage threshold determined with prolonged step currents.
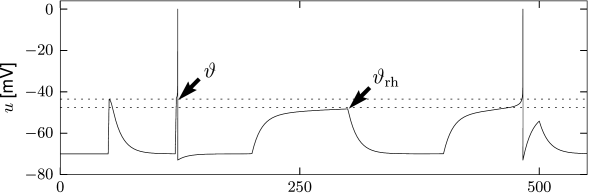
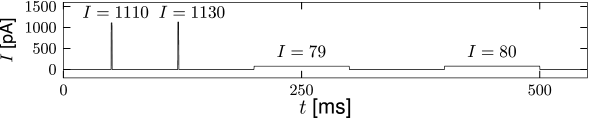
The critical current for initiation of repetitive firing corresponds to the voltage where the stable fixed point disappears, or \(\theta_{rh}=I_{c}R\). In the experimental literature, the critical current \(I_c=\theta_{rh}/R\) is called the 'rheobase' current. In the mathematical literature, it is called the bifurcation point.
Exponential Integrate-and-Fire Model
In the experimental integrate-and-fire model, the differential equation for the membrane potential is given by \[ \tau \frac{\mathrm{d}}{\mathrm{d}t}u=-(u-u_{rest})+\Delta_{T}\exp \left(\frac{u-\theta_{rh}}{\Delta_{T}}\right)+RI; \] (5.6)
The first term describe the leak of a passive membrane. The second term is an exponential nonlinearity with 'sharpness' parameter \(\Delta_{T}\) and 'threshold' \(\theta_{rh}\).
If the numerical threshold is chosen sufficiently high, \(\theta_{reset}\gg \theta+\Delta_{T}\), the upswing of the action potential for \(u\gg \theta+\Delta_{T}\) is so rapid, that it goes to infinity in an incredibly short time, so the exact value of \(\theta_{reset}\) does not play any role. \(\theta_{rh}\) is the threshold found with constant (rheobase) current.
Extracting the Nonlinearity from Data
Why we choose an exponential nolinearity rather than any other nonlinear dependence? After rescaling with the time constant \(\tau\), the nonlinearity \(\tilde{f}(u)=-f(u)/\tau\) is \[ \tilde{f}(u(t))=\frac{1}{C}I(t)-\frac{\mathrm{d}}{\mathrm{d}t}u(t); \]
where \(C=\tau/R\) can be intepreted as the capacity of the membrane.
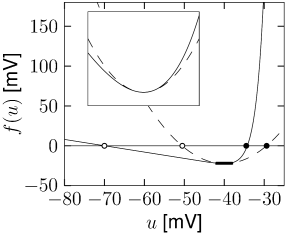
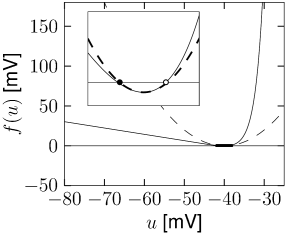
The slope of the curve at the resting potential is related to the membrane time constant \(\tau\) while the threshold parameter \(\theta_{rh}\) is the voltage at which the function \(\tilde{f}\) goes through its minimum.
From Hodgkin-Huxley to Exponential Integrate-and-Fire
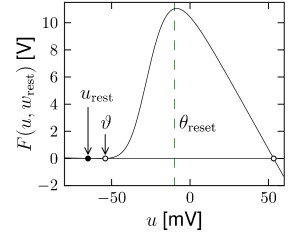
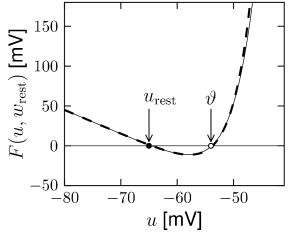
As long as we are only interested in the initiation phase of the action potential we can assume a fixed value \(w=w_{rest}\).
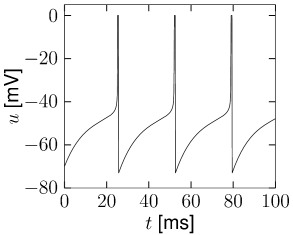
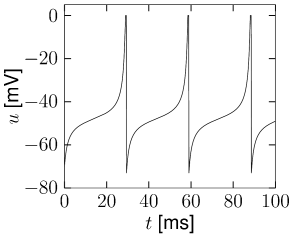
For constant \(w\), \[ \frac{\mathrm{d}u}{\mathrm{d}t}=F(u,w_{rest})+I=f(u)+I \] It has three zero-crossings: the first one (left) at \(u_{rest}\), corresponding to a stable fixed point; a second one (middle) which acts as a threshold \(\theta\); and a third one to the right, which is again a stable fixed point and limits the upswing of the action potential. The value of the reset threshold \(\theta_{reset}>\theta\) must be chosen between the second and third fixed point.
Replace the downswing of the action potential in the nonlinear integrate-and-fire model by an artificial reset of the voltage variable to a value \(u_{r}\) whenever \(u\) hits \(\theta_{reset}\).
Example: Exponential Activation of Sodium Channels
\[ C\frac{\mathrm{d}u}{\mathrm{d}t}=-g_{Na}[m_0(u)]^{3}h_{rest}(u-E_{Na})-g_{K}(n_{rest})^{4}(u-E_{K})-g_{L}(u-E_{L})+I, \] (5.15) Potassium and leak currents can now be summed up to a new effective leak term \(g^{eff}(u-E^{eff})\). In the voltage range close to the resting potential the driving force \((u-E_{Na})\) of the sodium current can be well approximated by \((u_{rest}-E_{Na})\). Then the only remaining nonlinearity on the right-hand-side of (5.15) arises from the \(m_0(u)\). For voltages around rest, \(m_0(u)\) has an exponential shape.
Quadratic Integrate and Fire
A specific instance of a nonlinear integrate-and-fire model is the quadratic model, \[ \tau\frac{\mathrm{d}}{\mathrm{d}t}u=a_0(u-u_{rest})(u-u_c)+RI, \] (5.16)
with \(a_0>0\) and \(u_c>u_{rest}\). The quadratic integrate-and-fire model is closely related to the so-called \(\Theta-\)neuron, a canonical type-I neuron model.
Canonical Type I model
We'll show a one-to-one relation between the quadratic integrate-and-fire model and the canonical type I phase model, \[ \frac{\mathrm{d}\phi}{\mathrm{d}t}=[1-\cos \phi]+\Delta I[1+\cos \phi]; \] (5.17) Denote by \(I_{\theta}\) the minimal current necessary for repetitive firing of the quadratic integrate-and-fire neuron. With a suitable shift of the voltage scale and constant current \(I=I_{\theta}+\Delta I\) the equation of the quadratic neuron model can then by cast into the form \[ \frac{\mathrm{d}u}{\mathrm{d}t}=u^{2}+\Delta I. \tag{5.18} \]
For \(\Delta I>0\) the voltage increases until it reaches the firing threshold \(\theta \gg 1\) where it is reset to a value \(u_r\ll -1\).
By the transformation \[ u(t)=\tan \left( \frac{\phi(t)}{2}\right). \tag{5.19} \] The differential equation (5.18) can be transformed into (5.17). Thus (5.19) with \(\phi(t)\) given by (5.17) is a solution to the differential equation of the quadratic integrate-and-fire neuron. The quadratic integrate-and-fire neuron is therefore (in the limit \(\theta \to \infty\) and \(u_r \to -\infty\)) equivalent to the genetic type I neuron (5.17).