About Bezier Curve
Bezier 曲线是本学期学过相当好用的东西. 本学期的Project2中涉及到Bezier曲线的部分大有可为. 搜索资料的过程中我找到了一个非常好的相关博客:
Fitting cubic Bézier curves | Raph Levien’s blog https://raphlinus.github.io/curves/2021/03/11/bezier-fitting.html
Project2中,问题的核心是:当曲线两端点处斜率确定,如何取控制点使得Bezier曲线与原曲线最接近. 下面读者将主要看到:千方百计凑字数造成的语义冗余、对上述博客的拙劣翻译、LaTeX文档转Markdown后丢失的图片标题(不想搞啦)、不明觉厉其实很naive的公式推导、由于公式过长导致显示出大问题(以后可能会想办法解决这个问题)、第一第三问丢失导致的没见过Project2的读者完全一头雾水的情况。
由于.png的透明格式,请在日间模式下阅读以获得最佳的阅读体验。
用三次样条插值得到的导数值控制贝塞尔曲线两个端点的斜率,用贝塞尔曲线画出图一曲线。结果如图四,其中参数 \(h\)的意义下面解释。图四中用不同的颜色画出了Curve1,Curve2和Curve3,并将插值的端点标出。
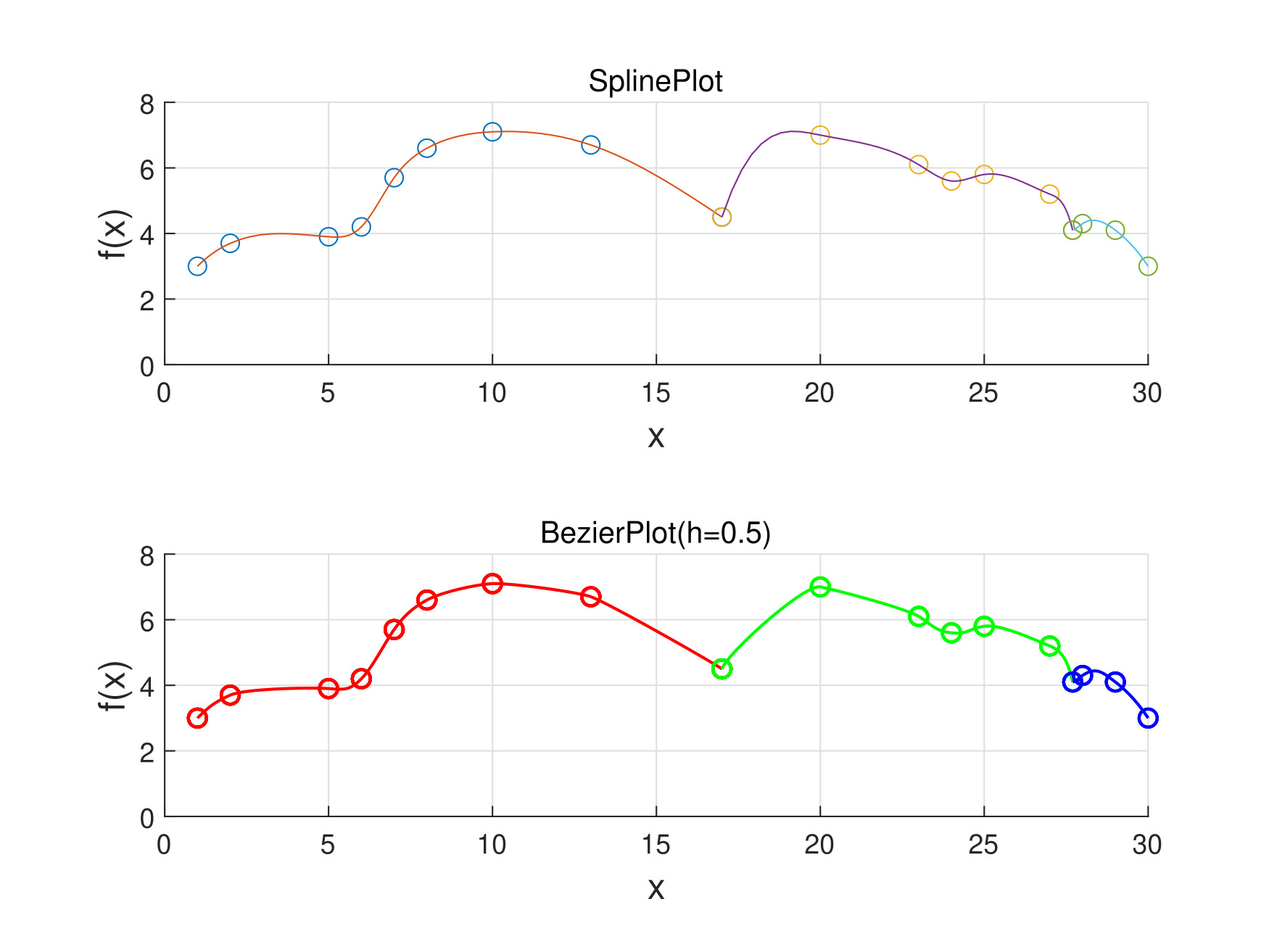
考虑到图一只给出了曲线的端点和端点处切线的斜率,我们引入参数 \(h_1\)和\(h_2\)。在 \(P_1=(x_i,y_i)\)和\(P_2=(x_{i+1},y_{i+1})\)之间绘制Bezier曲线时,\(h_1\)定义为第一个控制点 \(Q_1=(x_3,y_3)\)到\(P_1\)的距离,\(h_2\)定义为第二个控制点 \(Q_2=(x_4,y_4)\)到\(P_2\)的距离。设曲线在\(P_1\)处斜率为 \(p\),在 \(P_2\)处斜率为 \(q\)。则有 \[ \begin{aligned} x_3 & =x_1+\frac{h_1}{\sqrt{1+p^{2}}}, & y_3 & =y_1+\frac{ph_1}{\sqrt{1+p^{2}}}, \\ x_4 & =x_2-\frac{h_2}{\sqrt{1+q^{2}}}, & y_4 & =y_2-\frac{qh_2}{\sqrt{1+q^{2}}} \\ \end{aligned} \] 由Bezier曲线的计算公式 \[ \begin{aligned} b_x & =\frac{3h_1}{\sqrt{1+p^{2}}}, & b_y & =\frac{3ph_1}{\sqrt{1+p^{2}}}, \\ c_x & =3(x_2-x_1)-\frac{6h_1}{\sqrt{1+p^{2}}}-\frac{3h_2}{\sqrt{1+q^{2}}}, & c_y & =3(y_2-y_1)-\frac{6ph_1}{\sqrt{1+p^{2}}}-\frac{3qh_2}{\sqrt{1+q^{2}}} \\ d_x & =-2(x_2-x_1)+\frac{3h_1}{\sqrt{1+p^{2}}}+\frac{3h_2}{\sqrt{1+q^{2}}}, & d_y & =-2(y_2-y_1)+\frac{3ph_1}{\sqrt{1+p^{2}}}+\frac{3qh_2}{\sqrt{1+q^{2}}} \\ \end{aligned} \] 从而Bezier曲线 \[ \begin{aligned} x(t) & =x_1+b_xt+c_xt^{2}+d_xt^{3} \\ y(t) & =y_1+b_yt+c_yt^{2}+d_yt^{3} \\ \end{aligned} \] 记该曲线为 \(p_f\)。
\(h_1,h_2\)与Bezier曲线的关系
图五给出了当 \(h_1=h_2=h\)变动时 \(p_f\)的变化。注意当 \(h \to 0\)时 \[ \frac{y(t)-y_1}{x(t)-x_1}=\frac{p+[\frac{\sqrt{1+p^{2}}(y_2-y_1)}{h}-2p-\frac{\sqrt{1+p^{2}}q}{\sqrt{1+q^{2}}}]t+[-\frac{2\sqrt{1+p^{2}}(y_2-y_1)}{3h}+p+\frac{\sqrt{1+p^{2}}q}{\sqrt{1+q^{2}}}]t^{2}}{1+[\frac{\sqrt{1+p^{2}}(x_2-x_1)}{h}-2-\frac{\sqrt{1+p^{2}}}{\sqrt{1+q^{2}}}]t+[-\frac{2\sqrt{1+p^{2}}(x_2-x_1)}{3h}+1+\frac{\sqrt{1+p^{2}}}{\sqrt{1+q^{2}}}]t^{2}}\to p \] 即当 \(h\to 0\)时 \(p_f\)趋向于线性,而端点处仍然满足切线的斜率条件。
而当 \(h\)较大时,相应的 \(p_f\)会出现尖点,当 \(h\)继续增大时,相应的 \(p_f\)会出现自交点。事实上,1989年,Lasser提出了一种曲线曲线算法,通过使用de Casteljau算法对曲线的控制多边形进行细分来计算贝塞尔曲线的自交点。该方法需要在算法开始之前通过控制多边形的旋转角度之和来检查曲线与自交的可能性,即:当Bezier曲线的控制多边形外角和不大于 \(\pi\)时,Bezier曲线一定没有自交点。在图四的情况中,只有当线段\(P_1Q_1\)和线段\(P_2Q_2\)相交时, \(p_f\)才可能有自交点。
图五展示了使用不同方法绘制Curve2的图像,可以看到,关于h取值过小时过于接近线性的问题可以通过增加插值点避免。
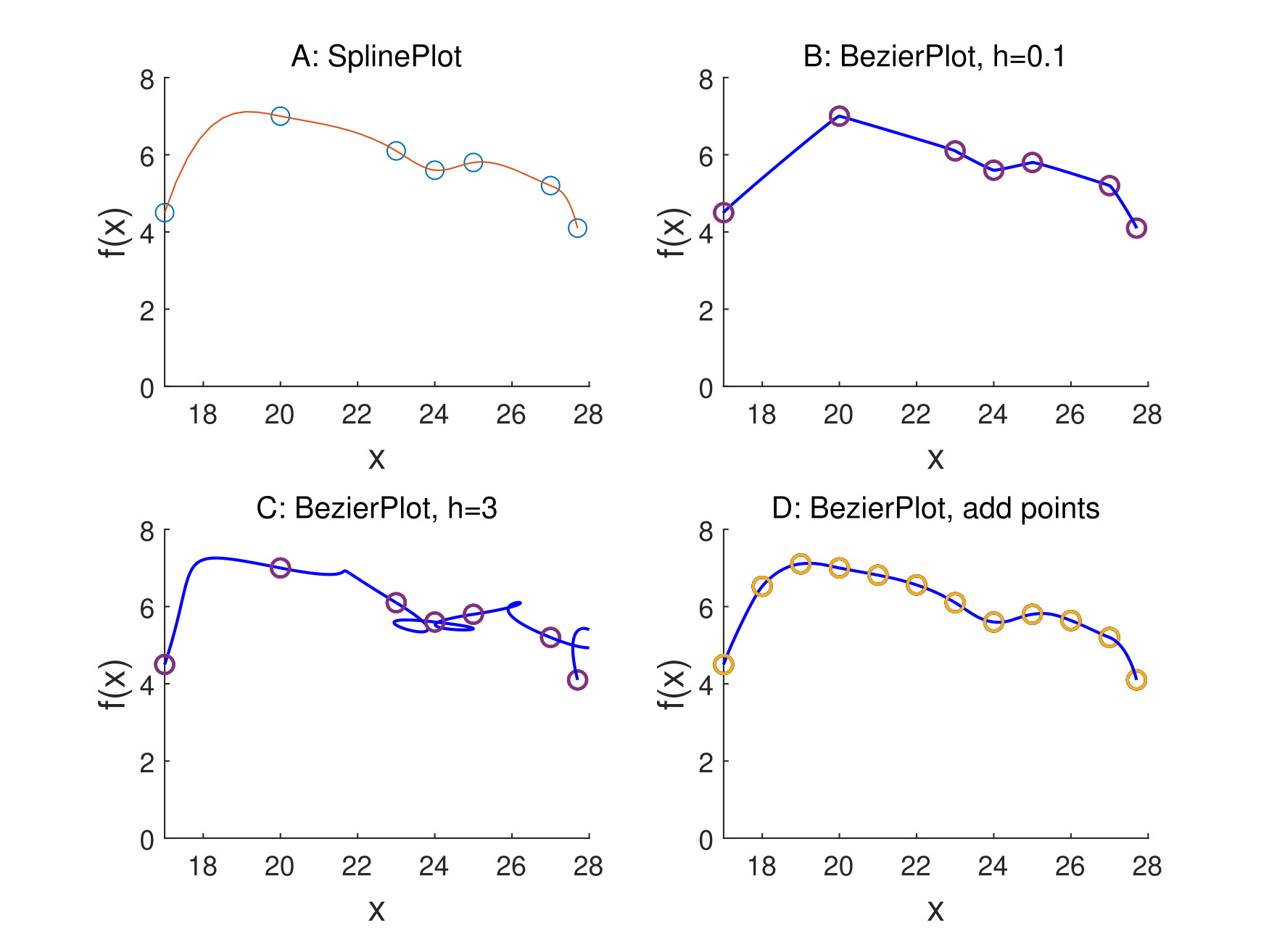
\(h_1,h_2\)的最佳取法
我们认为三次样条插值得到的曲线为标准曲线 \(s\),讨论 \(h_1\)和 \(h_2\)取何值时 \(p_f\)与 \(s\)最为“接近”。其中“接近”的不同含义分类讨论。
G2几何Hermite插值/Alvin Penner的三种方法
一个自然的想法是 \(p_f\)与 \(s\)在端点处的二阶导数值相等。\(p_f\)使用的是曲线的参数方程,由相关数学知识得 \[ \frac{\mathrm{d}^{2}y}{\mathrm{d}x^{2}}=\frac{y''(t)x'(t)-x''(t)y'(t)}{(x'(t))^{3}} \] 计算得到三次样条插值 \[ s(x)=y_1+p(x-x_1)+\biggl[\frac{3(y_2-y_1)}{(x_2-x_1)^{2}}-\frac{2p+q}{x_2-x_1}\biggr](x-x_1)^{2}+\biggl[\frac{p+q}{(x_2-x_1)^{2}}-\frac{2(y_2-y_1)}{(x_2-x_1)^{3}}\biggr](x-x_1)^{3} \] 那么相应端点二阶导数值相等得方程即为 \[ \begin{aligned} s''(x_1) & =\frac{y''(0)x'(0)-x''(0)y'(0)}{(x'(0))^{3}} \\ s''(x_2) & =\frac{y''(1)x'(1)-x''(1)y'(1)}{(x'(1))^{3}} \\ \end{aligned} \] 化简得到 \[ \begin{aligned} \frac{(1+p^{2})(h_2(p-q)+\sqrt{1+q^{2}}(p(x_1-x_2)-y_1+y_2))}{3h_1^{2}\sqrt{1+q^{2}}} & = \frac{(2p+q)(x_1-x_2)-3(y_1-y_2)}{(x_1-x_2)^{2}} \\ \frac{(1+q^{2})(h_1(p-q)-\sqrt{1+p^{2}}(q(x_1-x_2)-y_1+y_2))}{3h_2^{2}\sqrt{1+p^{2}}} & = \frac{-(p+2q)(x_1-x_2)+3(y_1-y_2)}{(x_1-x_2)^{2}} \\ \end{aligned} \] 经过消元可以得到关于 \(h_1\)和 \(h_2\)的一元四次方程,求该方程在一般情况下的解析解不具有实际意义。而特别的,当 \(p=q\),即两端点处切线斜率相等时,我们有 \[ h_1=h_2=\frac{\sqrt{1+p^{2}}}{3}(x_2-x_1) \]
对于 \(p \neq q\)的情况,\(h_1\)和 \(h_2\)可能根本没有解。即使有解,最小的正实数解也很可能较大,从而出现Bezier曲线自交的情况。例如 \((x_1,x_2,y_1,y_2,p,q)=(17,20,4.5,7.0,3,-0.198)\)时,\(h_1\)的最小正实数解为 \(3.162\),\(h_2\)的最小正实数解为 \(1.019\),此时曲线会出现明显的自交点。
查询相关资料后我们发现这是Carl de Boor et al在1987年的论文中分析的情况。由数据的不同,\(h_1,h_2\)可以有 \(0,1,2,3\)个正实数解。这篇论文还证明了 \(\text{dist}(s,p_f)=O(\lvert P_1P_2 \rvert^{6})\)。由于范数的等价性,我们可以任选 \(\text{dist}(s,p_f)\)的定义。在本文的例子中 $P_1P_2 $远大于 \(1\),故该估计不具有实际意义。
最近的一个结果是Alvin Penner于2019年发表的。他在文章中提出了三种方法。这些方法的优缺点总结可以见Rahp Levien's Blog。
利用有向面积和图像矩进行曲线拟合
该方法来源于Raph Levien's Blog。
首先改述这个问题,作数学上的简化。我们可以排除平移,均匀缩放和旋转,只需考虑从 \((0,0)\)到 \((1,0)\)的曲线,给定 \(\theta_0\)和 \(\theta_1\)。两条控制臂的长度设为 \(\delta_0\)和 \(\delta_1\)。我们仍记原曲线为 \(s\),记Bezier曲线为 \(p_f\)
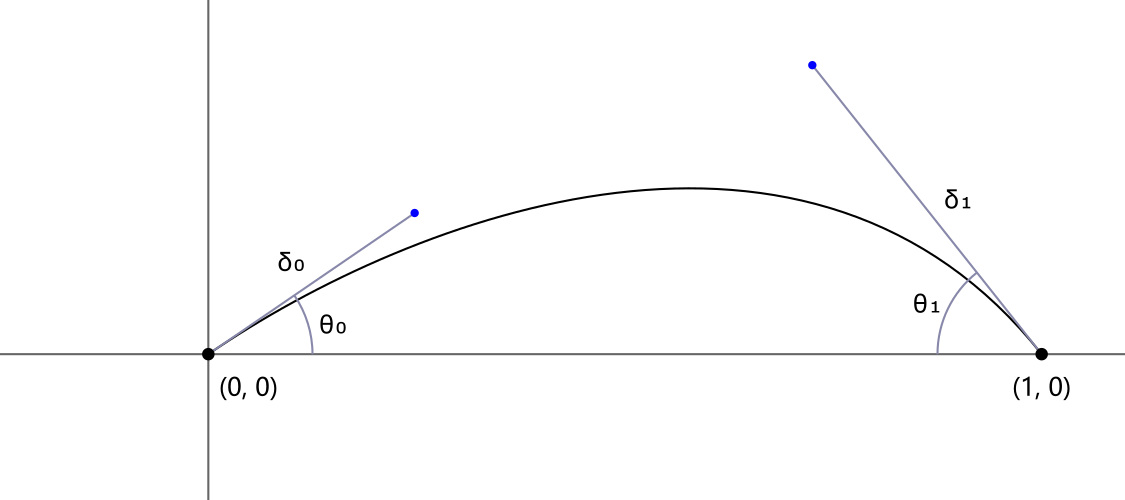
那么两个控制点的坐标为 \((\delta_0\cos \theta_0,\delta_0\sin \theta_0)\)和 \((1-\delta_1\cos \theta_1,\delta_1\sin \theta_1)\)。
三次样条插值(注意 \(q=-\tan \theta_1\)): \[ s(x)=\tan \theta_0 x-(2\tan \theta_0-\tan \theta_1)x^{2}+(\tan \theta_0-\tan \theta_1)x^{3} \]
Bezier曲线: \[ \begin{aligned} x(t) & =3\delta_0 \cos \theta_0 t+3(1-2\delta_0 \cos \theta_0+\delta_1\cos \theta_1)t^{2}+(-2+3\delta_0 \cos \theta_0-3\delta_1 \cos \theta_1)t^{3} \\ y(t) & =3\delta_0\sin \theta_0t-3(2\delta_0\sin \theta_0+\delta\sin \theta_1)t^2+3(\delta_0\sin \theta_0+\delta_1\sin \theta_1)t_3 \\ \end{aligned} \]
第一个做法是使得 \(p_f\)和 \(x\)轴围成的有向面积与 \(s\)和 \(x\)轴围成的有向面积相同,这是自然的。如图七所示,当围成面积不同时,拟合程度应当不会很高。

由Green公式,有 \[ \text{area}=\frac{3}{20}(2\delta_0\sin \theta_0+2\delta_1\sin \theta_1-\delta_0\delta_1\sin (\theta_0+\theta_1)) \]
对于现在的情况,
\[ \frac{1}{12}(\tan \theta_0+ \tan \theta_1)=\frac{3}{20}(2\delta_0\sin \theta_0+2\delta_1\sin \theta_1-\delta_0\delta_1\sin (\theta_0+\theta_1)) \]
从该式可以从给定的 \(\delta_0\)中解出唯一的 \(\delta_1\):
\[ \delta_1=\frac{\frac{5}{9}(\tan \theta_0+\tan \theta_1)-2\delta_0 \sin \theta_0}{2\sin \theta_1-\delta_0 \sin (\theta_0+\theta_1)} \]
第二个做法是利用图像矩(image moment)。在图六化简的情形中,图像矩即为x-矩。图八展示了图像矩对于曲线的影响。所有红色曲线都具有相同的有向面积。

由Green公式也可以化简计算 \[ \begin{aligned} \text{moment}_x & = \int_{0}^{1} x p_f(x) \mathrm{d}=\int_{0}^{1} x(t)y(t)x'(t) \mathrm{d}t \\ & = \frac{1}{280}(34\delta_0\sin \theta_0+50\delta_1\sin \theta_1+15\delta_0^{2}\sin \theta_0\cos \theta_0-15\delta_1^{2}\sin \theta_1\cos \theta_1 \\ & -\delta_0\delta_1(33\sin \theta_0\cos \theta_1+9\cos \theta_0\sin \theta_1)-9\delta_0^{2}\delta_1\sin (\theta_0+\theta_1)\cos \theta_0 \\ & +9\delta_0\delta_1^{2}\sin (\theta_0+\theta_1)\cos \theta_1) \end{aligned} \] 同样得到方程 \[ \begin{equation} \begin{aligned} \frac{\tan \theta_0}{30}+\frac{\tan \theta_1}{20} & = \frac{1}{280}(34\delta_0\sin \theta_0+50\delta_1\sin \theta_1+15\delta_0^{2}\sin \theta_0\cos \theta_0-15\delta_1^{2}\sin \theta_1\cos \theta_1 \\ & -\delta_0\delta_1(33\sin \theta_0\cos \theta_1+9\cos \theta_0\sin \theta_1)-9\delta_0^{2}\delta_1\sin (\theta_0+\theta_1)\cos \theta_0 \\ & +9\delta_0\delta_1^{2}\sin (\theta_0+\theta_1)\cos \theta_1) \end{aligned} \end{equation} \] 将(1)与(3)联立可以得到 \(\delta_0\)和 \(\delta_1\)的解。消元后得到的是两个一元四次方程,它们不一定有正实数解。在Raph Levien's Blog中提到了还需要考虑 \(\text{moment}_x\)的极值点(将 \(\delta_1\)用 \(\delta_0\)消去)。
将一般情况转化为简单情形
第二问的最后,我们求出 \(h_1,h_2\)与 \(\delta_0,\delta_1\)的关系。记 \(\displaystyle k=\frac{y_2-y_1}{x_2-x_1}\)
作坐标变换 \[ x'=\frac{x-x_1}{x_2-x_1}, \quad y'=\frac{y-y_1}{x_2-x_1}-\frac{y_2-y_1}{(x_2-x_1)^{2}}(x-x_1) \] 该变换将 \((x_1,y_1)\)和 \((x_2,y_2)\)映到 \((0,0)\)和 \((1,0)\),且保持比例与相切关系,我们有 \[ \tan \theta_0=p-k, \quad \tan \theta_1=-q+k \] 该变换的逆变换是 \[ x=x_1+(x_2-x_1)x', \quad y=y_1+(y_2-y_1)x'+(x_2-x_1)y' \] 那么就有 \[ \begin{aligned} h_1 & =\delta_0(x_2-x_1) \\ h_2 & =\delta_1(x_2-x_1) \\ \end{aligned} \]